This text shall serve as a high-level introduction to what I am doing in my master’s thesis. For a longer and more accurate description, it is referred to chapter 2.3 of the thesis.
Vector-Space embeddings
The field of computational Natural Language Processing has long noticed that hand-crafted algorithms are not really good at this job. Instead, all modern Machine Learning methods rely on vector-space embeddings, where every word of a text is converted into a high-dimensional vector, where the individual dimensions are optimized using the other text before and after the word“You shall know a word by the company it keeps”
(J. R. Firth, 1957). This results in word embeddings that not only improve the performance of basically all perceivable NLPNatural Language Processing tasks, but you can even “calculate” with these embeddings - as the famous word2vec paper[1]https://arxiv.org/abs/1310.4546 first showed: vec(king) - vec(man) + vec(woman) ~= vec(queen). Once you’ve reached this, there is a bunch of reasoning that can be expressed as geometric operations:
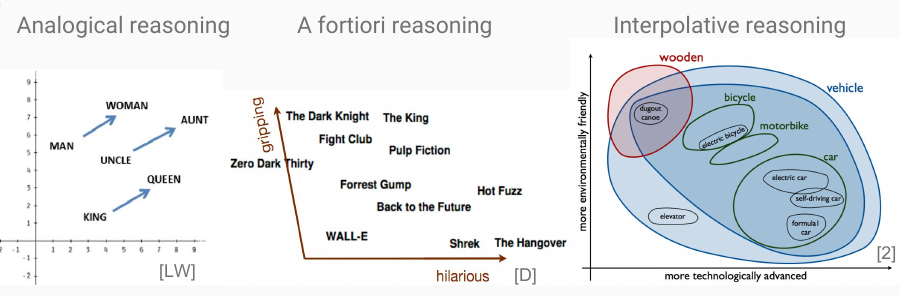
Conceptual Spaces
Conceptual Spaces take this a step further: In a CS, words or concepts get embedded in a high-dimensional embedding with interpretable dimensions. Where word embeddings as created by a neural network have arbitrary dimensions, in a CS these dimensions correspond to human concepts - in our king-queen-example from earlier, this would mean that there is one specific gender-dimension. In a conceptual space, concepts correspond to convex regions in this high-dimensional space, whereas specific instances are points or individual vectors. Take this example from Peter Gärdenfors, the inventor of conceptual spaces, as an example:
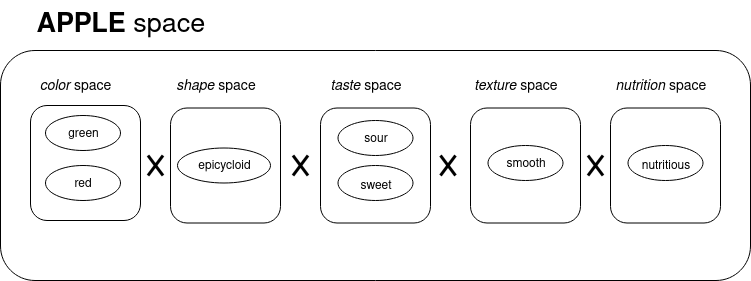
The concept of apple is something that is green-red-ish in color, roughly round in shape, somewhere between sour and sweet in taste, and so on. The concept of the apple is a region, and any specific apple should lie in this region.
Computational Spaces are useful as representation for objects and concepts, because many ways of logical reasoning have a geometric interpretation in this space. For example, an analogy may correspond to moving into the same direction. As very dumbed down example, the concept of a king relates to the concept of a queen the same way as the concept of uncle relates to the concept of aunt. Geometrically interpreted, this means “the vector that points from king to queen should be roughly equal in direction and length as the vector that points from uncle to aunt”. According to their inventor, Conceptual Spaces would be a useful layer in between connectionism, where everything is nothing above hardly interpretable chaotic firing of neurons, and symbolism, where logical reasoning can be guaranteed correct, however has the symbol grounding problem.
Generating Conceptual spaces
While in theory, conceptual spaces sound vastly useful and may be a solution to make even Large Language Models stop lying, in practice there is a huge problem: They need to be hand-crafted. This, obviously, would mean a lot of manual work. Because of this, the algorithm introduced by Derrac & Schockaert[2]https://www.sciencedirect.com/science/article/pii/S0004370215001034 introduces a way to generate them in a data-driven fashion. This algorithm works for cases, where there are many concept from a particular domain, each linked to its own text corpus. This may be the domain of movies, where the corresponding text corpora may consist of reviews from imdb, or the domain of courses with the given course descriptions as corpora, as I did in my thesis. The words (or embeddings) of these corresponding texts are then used to conceptualize the respective entity. The main idea behind this is described by Alshaikh, et al. [3]https://www.ijcai.org/proceedings/2020/494 as
words describing semantically meaningful features can be identified by learning for each candidate word
wa linear classifier which separates the embeddings of entities that havewin their description from the others.
So, what we do is to represent each entity using its text in a high-dimensional space, where the axes correspond to (the result of dimensionality reduction methods on) the significance of respective words in the entity’s description. To then get the actually salient words in the texts, we subsequently filter these by training a linear classifier for each candidate that seperates the vector representations of the entities that contain the term from those that do not. If this classifier can achieve good accuracy, we assume that the candidate term captures a salient feature: If the entity representations can clearly be split into those with that word and words without it, that word must be a feature of a certain subset of the entities. The direction of its corresponding dimension is then characterized by the orthogonal of the classifier’s separatrix. Finally, we only need to cluster these candidate dimensions and find representative axis names for the directions, using the respectively clustered dimensions. We can then re-embed the words into a space of semantic directions by calculating their distance to each of the feature direction separatrices, resulting in something like a conceptual space.
If that description was not clear enough, consider the following plotThe code to generate this plot is available here which hopefully explains this more vividly:
Linear Support Vector Machines have the property to find a linear hyperplane that best separates some positive from negative samples. What’s good about that is, that you can interpret the distance of a sample from the hyperplane as the degree of prototypicality for that respective class. Thus, if we project each sample coordinate onto the orthogonal of that hyperplane